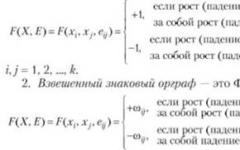Оптимизация: Теория, примеры, задачи Год: 2000 Автор: Галеев Е.М., Тихомиров В.М. Жанр: Учебное пособие Издательство: Едиториал УРСС ISBN: 5-8360-0041-7 Язык: Русский Формат: DjVu Качество: Отсканированные страницы + слой распознанного текста Интерактивное оглавление: Нет Количество страниц: 160 разворотов по 2 стр. Описание: Книга посвяшена важнейшим проблемам оптимизации. Она построена на базе преподавания теории оптимизации на механико-математическом факультете МГУ. В основе ее лежат курсы, прочитанные и 1998/99 годах Э.М.Галееиым (Главы 1-5) и В.М.Тихомировым (Глава 6). Рассматриваются фрагменты следующих разделов теории экстремальных задач: линейного и выпуклого программирования, математического программирования, классического вариационного исчисления и оптимального управления. Приводятся как необходимые, так и достаточные условия экстремума. Для изучения этих разделов в необходимом объеме даются элементы функционального и выпуклого анализа. В каждом параграфе после теоретической части приводятся примеры решения задач, предлагаются задачи для решения на семинарах, контрольных и для домашних задании. Дается обзор общих методов теории экстремума. Для студентов вузов по специальностям «Математика», «Прикладная математика», а также для аспирантов, преподавателей и научных работников. Примеры страниц Оглавление
М.: Эдиториал УРСС, 2000 г. , 320 с.
Книга посвящена важнейшим проблемам оптимизации. Она построена на базе преподавания теории оптимизации на механико-математическом факультете МГУ. В основе ее лежат курсы, прочитанные в 1998/99 годах Э. М. Галеевым (Главы 1-5) и В. М. Тихомировым (Глава 6). Рассматриваются фрагменты следующих разделов теории экстремальных задач: линейного и выпуклого программирования, математического программирования, классического вариационного исчисления и оптимального управления. Приводятся как необходимые так и достаточные условия экстремума. Для изучения этих разделов в необходимом объеме даются элементы функционального и выпуклого анализа. В каждом параграфе после теоретической части приводятся примеры решения задач, предлагаются задачи для решения на семинарах, контрольных и для домашних заданий. Даётся обзор общих методов теории экстремума.
Для студентов вузов по специальностям «Математика», «Прикладная математика», а также для аспирантов, преподавателей и научных работников.
Оглавление:
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ.
Конечномерные задачи без ограничений.
Конечномерные гладкие задачи с равенствами.
Конечномерные гладкие задачи с равенствами и неравенствами.
Выпуклые задачи.
Элементы функционального анализа.
Гладкая задача без ограничений.
Гладкая задача с равенствами.
Гладкая задача с равенствами и неравенствами.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.
Симплекс-метод.
Двойственность в линейном программировании.
Обоснование симплекс-метода.
Методы нахождения начальной крайней точки.
Транспортная задача.
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ.
Простейшая задача классического вариационного исчтсления.
Задача Больца.
Задача с подвижными концами.
Изопериметрическая задача.
Задача со старшими производными.
Задача Лагранжа.
ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ.
Принцип максимума Понтрягина в общем случае.
Формулировка и доказательство принципа максимума.
Избранные задачи оптимального управления.
УСЛОВИЯ ВТОРОГО ПОРЯДКА В ВАРИАЦИОННОМ ИСЧИСЛЕНИИ.
Простейшая задача вариационного исчисления.
ОБЩАЯ ТЕОРИЯ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ.
Введение.
Принцип Лагранжа для необходимых условий экстремума.
Возмущения экстремальных задач.
Расширение вариационных задач и существование решений.
Алгоритмы оптимизации.
Скачать файл

- 1.74 МБ
- добавлен 12.09.2008
В книге собрано примерно 700 задач на отыскание экстремумов для конечномерного случая, для задач классического вариационного исчисления, оптимального управления и выпуклого программирования. Содержатся элементы функционального анализа, дифференциального исчисления и выпуклого анализа.
В книге приведены теория, необходимая дл...

- 2.61 МБ
- добавлен 08.02.2011
Учебное пособие М.: Наука, 1984. - 288с.
В книге собрано примерно 700 задач на отыскание экстремумов для конечномерного случая, для задач классического вариационного исчисления, оптимального управления и выпуклого программирования. Содержатся элементы функционального анализа, дифференциального исчисления и выпуклого анализа....

- 605.67 КБ
- добавлен 26.08.2011
Барнаул: Изд-во Алтайского гос. университета, 2005. - 43 с. .
Классическая теория оптимизации.
Задачи на основные понятия, связанные с экстремальными задачами….
Безусловная оптимизация. Гладкие задачи без ограничений.
дкие конечномерные задачи с ограничениями типа равенств.
дкие задачи с ограничениями типа ра...

- 1.15 МБ
- добавлен 05.11.2010
К.: ТвіМС, 2004. – 240 с.
Учебное пособие по теории выпуклого анализа и математического программирования рассчитан на студентов математических факультетов университетов, изучающих курсы "Методы оптимизации", "Теория выбора и принятие решений", "Методы негладкого анализа и оптимизация".
Разделы пособия:
1. Экстремаль...

- 1.46 МБ
- добавлен 25.09.2011
Pittsburgh, Carnegie Mellon University, 2006. 349p.
Учебник по методам оптимизации с приложениями из области финансов и экономики (указаны в скобках). Включает линейное программирование (задачи максимизации потока доходов и выявления ценового арбитража), нелинейное программирование (оценка волатильности), квадратичного...

- 28.51 КБ
- добавлен 25.01.2012
угату, фирт, Хасанов, 2011-2012 год.
Формулирование задач оптимизации.
Безусловная оптимизация.
Одномерная безусловная оптимизация.
Многомерная безусловная оптимизация.
Условная оптимизация.
Линейное программирование.
Нелинейное программирование.
Оптимизация на графах.
Задачи на отыскание наибольших и наименьших величин являются актуальными на протяжении всей истории развития человечества. Особенное значение они приобретают в настоящее время, когда возрастает важность в наиболее эффективном использовании природных богатств, людских ресурсов, материальных и финансовых средств. Все это приводит к необходимости отыскивать наилучшее, или как говорят, оптимальное решение того или иного вопроса.
Первые задачи на максимум и минимум были поставлены и решены в глубокой древности, когда математика только зарождалась как наука. Теория экстремальных задач начала создаваться в начале 17 века, и затем она активно развивалась вплоть до наших дней, включая в свою орбиту крупнейших математиков таких как Ферма, Ньютон, Лейбниц, Бернулли, Лагранж, Эйлер, Пуанкаре, фон Нейман, Канторович, Понтрягин и других. В наше время невозможно мыслить себе полноценное математическое образование без элементов теории экстремума.
Книга состоит из 6 глав. Первые пять глав, составляющих первую часть, написаны Э.М.Галеевым. Они содержат материал курсов оптимизации, читаемых на курсах лекций по методам оптимизации, линейному программированию, оптимальному управлению и вариационному исчислению на механико-математическом факультете Московского государственного университета, а также в некоторых институтах естественно научного профиля. Данный курс лекций был разработан целым рядом профессоров и преподавателей механико-математического факультета МГУ. На начальном этапе курс формировался усилиями В.М.Алексеева, В.М.Тихомирова, С.В.Фомина. Методическая разработка доказательств, а так же подбор и составление задачного материала во многом были проведены Э.М.Галеевым. При написании этих глав использовался материал, содержащийся в ранее опубликованных книгах: (АТФ) Алексеев В.М., Тихомиров В.М., Фомин С.В. "Оптимальное управление", М.: Наука, 1979; (АГТ) Алексеев В.М., Галеев Э.М., Тихомиров В.М. "Сборник задач по оптимизации", М.: Наука, 1984; (ГТ) Галеев Э.М., Тихомиров В.М. "Краткий курс теории экстремальных задач", М.: Изд-во МГУ, 1989. Эта часть книги является расширением вариантом пособия Галеева Э.М. "Курс лекций по вариационному исчислению и оптимальному управлению", М.: Изд-во мехмата МГУ, 1996. Она предназначена для курсов, включающих элементы теории экстремума любого уровня и приспособлена к действующим ныне программам. Все чертежи в LATEX" 2\e выполнены Альфирой Галеевой.
В этой части рассматриваются следующие разделы теории экстремальных задач: задачи без ограничений, гладкие задачи с ограничениями типа равенств и неравенств, линейное программирование, классическое вариационное исчисление, оптимальное управление, необходимые и достаточные условия экстремума в классическом вариационном исчислении.
При изучении данных разделов требуется знание основ математического анализа и линейной алгебры, изучаемых на первых двух курсах технических и педагогических вузов, университетов. Предполагается, что читатели знакомы с элементарными приемами дифференцирования и интегрирования функций, умеют решать простейшие дифференциальные уравнения, знакомы с элементарными навыками работы с матрицами (умножением, транспонированием, нахождением обратной). Все остальные используемые в курсе математические понятия подробно определяются.
В первой главе рассматриваются задачи без ограничений, задачи с ограничениями типа равенств, с ограничениями типа равенств и неравенств для числовых функций n переменных и в нормированных пространствах. Для каждого типа задач приводятся решения соответствующих примеров. Одним из примеров является старинная задача Аполлония о нормалях к эллипсу. Методами теории экстремальных задач решается задача из курса алгебры о приведении квадратичной формы к главным осям. Большое внимание уделяется выпуклым задачам. Даются элементы выпуклого анализа, причем выпуклый анализ в зависимости от уровня математической подготовки читателя может рассматриваться как в конечномерных пространствах, так и в линейных нормированных пространствах, вводится понятие субдифференциала и доказывается теорема Куна--Таккера. В этой же главе даются некоторые элементы функционального анализа и дифференциального исчисления в нормированных пространствах.
Вторая глава посвящена линейному программированию. В ней вначале даются постановки задач линейного программирования, правило решения задач в канонической форме по симплекс-методу, приводятся с решениями примеры. Вводится понятие двойственности, затем проводится строгое обоснование симплекс-метода, дается ряд методов нахождения первоначальной крайней точки. Полученные навыки применяются к некоторым наиболее известным типам задач линейного программирования -- транспортным задачам и задачам о назначении. Основная цель при этом -- ознакомление студентов с имеющимися методами решения задач линейного программирования и проведение обоснования этих методов. Обоснование проводится таким образом, чтобы для решения подобных задач в дальнейшем возможно было бы самостоятельно создать метод решения и провести его обоснование. В пособии приведены доказательства теоремы существования решений и теоремы двойственности, позволяющие более глубоко понять данный курс.
В третьей главе приводятся следующие элементарные задачи классического вариационного исчисления: простейшая задача, задача Больца, изопериметрическая задача. Все эти задачи являются частным случаем более общей задачи Лагранжа. Как частный случай задачи Лагранжа рассматриваются задача с подвижными концами и задача со старшими производными.
В четвертой главе рассматриваются задачи оптимального управления. Приводится формулировка и доказательство принципа максимума Понтрягина в общем случае, а также принципа максимума для задачи со свободным концом. Решаются простейшая задача о быстродействии, задача Ньютона и ряд других задач оптимального управления.
В пятой главе даны в простейшей задаче классического вариационного исчисления.
Глава 6, составляющая вторую часть, написана В.М.Тихомировым и посвящена обзору всей теории экстремальных задач с единых современных позиций. Она основана на записях курса лекций, читавшегося Тихомировым В.М. на механико-математическом факультете МГУ осенью 1998 года. В ней в сжатой форме выражено воззрение на теорию экстремальных задач, составившее стержень книг Иоффе А.Д., Тихомиров В.М. "Теория экстремальных задач", М.: Наука, 1974 и Алексеев В.М., Тихомиров В.М., Фомин С.В. "Оптимальное управление", М.: Наука, 1979.
Эта часть рассчитана на преподавателей вузов и университетов (в особенности, на ведущих занятия по курсам оптимизации), студентов старших курсов университетов и научных работников, интересующихся проблемами теории экстремума и местом, которое занимает этот раздел анализа в современной математике. Глава 6 написана в надежде на то, что она поспособствует модернизации курсов оптимизации в будущем.
Глава 6 состоит из пяти параграфов, посвященных принципу Лагранжа для необходимых условий экстремума, возмущениям экстремальных задач, существованию решений, алгоритмам оптимизации. Отдельный пятый параграф посвящен решению конкретных задач.
Э.М.Галеев, В.М.Тихомиров
| Предисловие | |||
| ЧАСТЬ I | |||
| Введение | |||
| Глава 1. | Экстремальные задачи | ||
| 1. | Конечномерные задачи без ограничений | ||
| 1.1. | Постановка задачи | ||
| 1.2. | Необходимые и достаточные условия экстремума | ||
| 1.3. | Правило решения | ||
| 1.4. | Примеры | ||
| 1.5. | Задачи, упражнения | ||
| 2. | Конечномерные гладкие задачи с равенствами | ||
| 2.1. | Постановка задачи | ||
| 2.2. | Необходимые и достаточные условия экстремума | ||
| 2.3. | Правило решения | ||
| 2.4. | Примеры | ||
| 2.5. | Задача Аполлония | ||
| 2.6. | Задачи | ||
| 3. | Конечномерные гладкие задачи с равенствами и неравенствами | ||
| 3.1. | Постановка задачи | ||
| 3.2 | Необходимые и достаточные условия экстремума | ||
| 3.3. | Правило решения | ||
| 3.4. | Примеры | ||
| 3.5. | Задачи | ||
| 4. | Выпуклые задачи | ||
| 4.1. | Элементы выпуклого анализа. Субдифференциал | ||
| 4.2. | Теоремы отделимости | ||
| 4.3. | Задачи без ограничений | ||
| 4.4. | Задачи с ограничением | ||
| 4.5. | Задача выпуклого программирования | ||
| 4.6. | Задачи, упражнения | ||
| 5. | Элементы функционального анализа | ||
| 5.1. | Нормированные и банаховы пространства | ||
| 5.2. | Определения производных | ||
| 5.3. | Некоторые теоремы дифференциального исчисления в нормированных пространствах | ||
| 5.4. | Дополнительные сведения из алгебры и функционального анализа | ||
| 5.5. | Задачи | ||
| 6. | Гладкая задача без ограничений | ||
| 6.1. | Постановка задачи | ||
| 6.2. | |||
| 6.3. | Необходимые и | ||
| 7. | Гладкая задача с равенствами | ||
| 7.1. | Постановка задачи | ||
| 7.2. | Необходимые условия I порядка | ||
| 7.3. | |||
| 7.4. | Достаточные условия II порядка | ||
| 8. | Гладкая задача с равенствами и неравенствами | ||
| 8.1. | Постановка задачи | ||
| 8.2. | Необходимые условия I порядка | ||
| 8.3. | Необходимые условия II порядка | ||
| 8.4. | Достаточные условия II порядка | ||
| Ответы к задачам главы 1 | |||
| Глава 2. | Линейное программирование | ||
| 1. | Симплекс-метод | ||
| 1.1. | Постановки задач. Геометрическая интерпретация | ||
| 1.2. | Правило решения задач по симплекс-методу | ||
| 1.3. | Примеры | ||
| 1.4. | Задачи | ||
| 2. | Двойственность в линейном программировании | ||
| 2.1. | Элементы выпуклого анализа. Преобразование Лежандра | ||
| 2.2. | Примеры | ||
| 2.3. | Вывод двойственных задач | ||
| 3. | Обоснование симплекс-метода | ||
| 3.1. | Теоремы существования, двойственности, критерий решения | ||
| 3.2. | Свойства множества допустимых точек | ||
| 3.3. | Доказательство симплекс-метода | ||
| 4. | |||
| 4.1. | Переход к решению двойственной задачи | ||
| 4.2. | Метод искусственного базиса | ||
| 4.3. | Примеры | ||
| 4.4. | Задачи | ||
| 5. | Транспортная задача | ||
| 5.1. | Постановка задачи | ||
| 5.2. | Особенности задачи | ||
| 5.3. | Методы нахождения начальной крайней точки | ||
| 5.4. | Метод потенциалов | ||
| 5.5. | Примеры транспортных задач | ||
| 5.6. | Задача двойственная к транспортной задаче | ||
| 5.7. | Обоснование метода потенциалов решения тран-спортной задачи | ||
| 5.8. | Задача о назначении. Пример | ||
| 5.9. | Задачи | ||
| Ответы к задачам главы 2 | |||
| Глава 3. | Вариационное исчисление | ||
| 1. | |||
| 1.1. | Постановка задачи | ||
| 1.2. | Вывод уравнения Эйлера с помощью основной леммы вариационного исчисления | ||
| 1.3. | Вывод уравнения Эйлера с помощью леммы Дю-буа-Реймона | ||
| 1.4. | Векторный случай | ||
| 1.5. | Интегралы уравнения Эйлера | ||
| 1.6. | Примеры | ||
| 1.7. | Задачи | ||
| 2. | Задача Больца | ||
| 2.1. | Постановка задачи | ||
| 2.2. | |||
| 2.3. | Многомерный случай | ||
| 2.4. | Пример | ||
| 2.5. | Задачи Больца | ||
| 3. | Задача с подвижными концами | ||
| 3.1. | Постановка задачи | ||
| 3.2. | Hеобходимые условия экстремума | ||
| 3.3. | Пример | ||
| 3.4. | Задачи с подвижными концами | ||
| 4. | Изопериметрическая задача | ||
| 4.1. | Постановка задачи | ||
| 4.2. | Необходимое условие экстремума | ||
| 4.3. | Пример | ||
| 4.4. | Задача Дидоны | ||
| 4.5. | Изопериметрические задачи | ||
| 5. | Задача со старшими производными | ||
| 5.1. | Постановка задачи | ||
| 5.2. | Необходимое условие экстремума | ||
| 5.3. | Пример | ||
| 5.4. | Задачи со старшими производными | ||
| 6. | Задача Лагранжа | ||
| 6.1. | Постановка задачи | ||
| 6.2. | Необходимые условия экстремума | ||
| 6.3. | Примеры | ||
| 6.4. | Вывод уравнения Эйлера--Пуассона из теоремы Эй-лера--Лагранжа | ||
| 6.5. | Задачи Лагранжа | ||
| Ответы к задачам главы 3 | |||
| Глава 4. | |||
| 1. | Принцип максимума Понтрягина в общем случае | ||
| 1.1. | Постановка задачи | ||
| 1.2. | Формулировка теоремы | ||
| 1.3. | Доказательство | ||
| 1.4. | Пример | ||
| 2. | Формулировка и доказательство принципа максимума Понтрягина для задачи со свободным концом | ||
| 3. | Избранные задачи оптимального управления | ||
| 3.1. | Простейшая задача о быстродействии | ||
| 3.2. | Аэродинамическая задача Ньютона | ||
| 3.3. | Примеры задач оптимального управления | ||
| 3.4. | Задачи оптимального управления | ||
| Ответы к задачам главы 4 | |||
| Глава 5. | Условия второго порядка в вариационном исчислении | ||
| 1. | Простейшая задача вариационного исчисления | ||
| 1.1. | Сильный и слабый экстремум | ||
| 1.2. | Пример слабого, но не сильного экстремума | ||
| 1.3. | Условия Лежандра, Якоби, Вейерштрасса | ||
| 1.4. | Необходимые и достаточные условия слабого и сильного экстремума | ||
| 1.5. | Правило решения | ||
| 1.6. | Примеры | ||
| 1.7. | Задачи | ||
| Ответы к задачам главы 5 | |||
| Список литературы к части I | |||
| ЧАСТЬ II | |||
| Глава 6. | Общая теория экстремальных задач | ||
| 0. | Введение | ||
| 0.1. | Основные темы и принципы общей теории экстремума | ||
| 0.2. | Классы экстремальных задач | ||
| 0.3. | О базе теории | ||
| 1. | Пpинцип Лагранжа для необходимых условий экстремума | ||
| 1.1. | Формулировка принципа Лагранжа для гладко-выпуклых задач | ||
| 1.2. | Доказательство принципа Лагранжа для гладко-выпуклых задач | ||
| 1.3. | Следствия принципа Лагранжа | ||
| 2. | Возмущения экстремальных задач | ||
| 2.1. | Возмущения в математическом программировании | ||
| 2.2. | Простейшая задача классического вариационного исчисления | ||
| 3. | Расширение вариационных задач и существование решений | ||
| 3.1. | Расширение вариационных задач | ||
| 3.2. | Теоремы существования в задачах вариационного исчисления | ||
| 4. | Алгоритмы оптимизации | ||
| 4.1. | Алгоритмы минимизации квадратичной функции | ||
| 4.2. | Метод центрированных сечений и метод эллипсоидов | ||
| 5. | Приложения общей теории к решению конкретных задач | ||
| 6. | Заключительные замечания | ||
| Список литературы к части II | |||
| Список обозначений | |||
| Предметный указатель | |||
| Сведения об авторах | |||
Галеев Эльфат Михайлович , доктор физико-математических наук, профессор кафедры общих проблем управления механико-математического факультета Московского государственного университета им. М.В.Ломоносова. Автор более 75 научных работ, в том числе ряда монографий по теории экстремальных задач. Научные интересы: теория приближений, теория экстремальных задач.
Тихомиров Владимир Михайлович , доктор физико-математических наук, профессор, заведующий кафедрой общих проблем управления механико-математического факультета Московского государственного университета им. М.В.Ломоносова. Автор более 140 научных работ, в том числе ряда монографий по теории экстремальных задач и теории приближений. Научные интересы: теория приближений, теория экстремальных задач.
 Галеев
Эльфат Михайлович
Галеев
Эльфат Михайлович
Доктор физико-математических наук, профессор кафедры общих проблем управления механико-математического факультета Московского государственного университета имени М. В. Ломоносова. Специалист в области теории аппроксимации, функционального анализа, теории экстремальных задач и методики преподавания элементарной математики.
 Тихомиров
Владимир Михайлович
Тихомиров
Владимир Михайлович
Доктор физико-математических наук, заведующий кафедрой общих проблем управления механико-математического факультета Московского государственного университета имени М. В. Ломоносова, почетный профессор МГУ. Автор более 250 научных работ и более 20 монографий и учебников.
Э.М. Га леев В.М.Тихомиров ОПТИМИЗАЦИЯ > Теория > Примеры > Задачи Эдиториал У PC С Москва 2000
ББК22.18я73 Настоящее tiiikinuc осуществлено при финансовой поддержке Российского фонда фундаментальных исследовании (проект № 98-01-14126) Галеев Эльфат Михайлович, Тихомиров Владимир Михайлович Оптимизация: теория, примеры, задачи. - М: Элиториал УРСС, 2000. - 320 с. ISBN 5-K36O43O41-7 Книга посвяшена важнейшим проблемам оптимизации. Она построе- построена на базе преподавания теории оптимизации на механико-математическом факультете МГУ. В основе ее лежат курсы, прочитанные и 1998/99 юлах Э. М. Галееиым (Гманы 1-5) и В. М. Тихомировым (["лава 6). Рассматривают- Рассматриваются фрагменты следующих разделов теории экстремальных задач: линейного и выпуклого программирования, математического программирования, класси- классического вариационного исчисления и оптимального управления. Приводятся как необходимые так и достаточные условия экстремума. Для изучения этих разделов в необходимом объеме даются элементы функционального и вы- выпуклого анализа. В каждом параграфе после теоретической части приводятся примеры решения задач, предлагаются задачи для решения на семинарах, контрольных и для домашних задании. Дается обзор общих методов теории экстремума. Для студентов вузов по специальностям «Математика», «Прикладная математика», а также для аспирантов, преподавателей и научных работников. 785836м000417 ISBN 5-8360-0041-7 О Э. М. Галеев, В. М.Тихомиров, 2000 © Эднторнал УРСС, 2000 Предисловие Задачи на отыскание наибольших и наименьших величин являют- являются актуальными на протяжении всей истории развития человечества. Особенное значение они приобретают в настоящее время, когда воз- возрастает важность в наиболее эффективном использовании природных богатств, людских ресурсов, материальных и финансовых средств. Все это приводит к необходимости отыскивать наилучшее, или как говорят, оптимальное решение того или иного вопроса. Первые задачи на максимум и минимум были поставлены и решены в глубокой древности, когда математика только зарождалась как наука. Теория экстремальных задач начала создаваться в начале 17 века, и за- затем она активно развивалась вплоть до наших дней, включая в свою орбиту крупнейших математиков таких как Ферма, Ньютон, Лейбниц, Бернулли, Лагранж, Эйлер, Пуанкаре, фон Нейман, Канторович, Пон- трягин и других. В наше время невозможно мыслить себе полноценное математическое образование без элементов теории экстремума. Книга состоит из 6 глав. Первые пять глав, составляющих пер- первую часть, написаны Э. М. Галеевым. Они содержат материал курсов оптимизации, читаемых на курсах лекций по методам оптимизации, линейному программированию, оптимальному управлению и вариаци- вариационному исчислению на механико-математическом факультете Москов- Московского государственного университета, а также в некоторых институтах естественно научного профиля. Данный курс лекций был разработан целым рядом профессоров и преподавателей механико-математического факультета МГУ. На начальном этапе курс формировался усилиями В.М.Алексеева, В.М.Тихомирова, С.В.Фомина. Методическая разра- разработка доказательств, а так же подбор и составление задачного материала во многом были проведены Э. М. Галеевым. При написании этих глав использовался материал, содержащийся в ранее опубликованных книгах: (АТФ) Алексеев В. М., Тихомиров В. М., Фомин СВ. «Оптимальное управление», М.: Наука, 1979; (АГТ) Алексеев В. М., Галеев Э. М., Тихомиров В. М. «Сборник задач по оптимизации», М.: Наука, 1984; (ГТ) Галеев Э. М., Тихомиров В. М. «Краткий курс теории экстремальных задач», М.: Изд-во МГУ, 1989. Эта часть книги является расширением вариантом пособия Галеева Э. М. «Курс лекций по вариационному исчи- исчислению и оптимальному управлению», М.: Изд-во мехмата МГУ, 1996. Она предназначена для курсов, включающих элементы теории экстрему- экстремума любого уровня и приспособлена к действующим ныне программам. Все чертежи в LATEX"e 7е выполнены Альфирой Галеевой. В этой части рассматриваются следующие разделы теории экстре- экстремальных задач: задачи без ограничений, гладкие задачи с ограничениями
4 Предисловие типа равенств и неравенств, линейное программирование, классичес- классическое вариационное исчисление, оптимальное управление, необходимые и достаточные условия экстремума в классическом вариационном исчис- исчислении. При изучении данных разделов требуется знание основ математиче- математического анализа и линейной алгебры, изучаемых на первых двух курсах технических и педагогических вузов, университетов. Предполагается, что читатели знакомы с элементарными приемами дифференцирования и интегрирования функций, умеют решать простейшие дифференци- дифференциальные уравнения, знакомы с элементарными навыками работы с ма- матрицами (умножением, транспонированием, нахождением обратной). Все остальные используемые в курсе математические понятия подробно определяются. В первой главе рассматриваются задачи без ограничений, задачи с ограничениями типа равенств, с ограничениями типа равенств и не- неравенств для числовых функций п переменных и в нормированных пространствах. Для каждого типа задач приводятся решения соответ- соответствующих примеров. Одним из примеров является старинная задача Аполлония о нормалях к эллипсу. Методами теории экстремальных за- задач решается задача из курса алгебры о приведении квадратичной формы к главным осям. Большое внимание уделяется выпуклым задачам. Дают- Даются элементы выпуклого анализа, причем выпуклый анализ в зависимости от уровня математической подготовки читателя может рассматриваться как в конечномерных пространствах, так и в линейных нормирован- нормированных пространствах, вводится понятие субдифференциала и доказывается теорема Куна-Таккера. В этой же главе даются некоторые элементы функционального анализа и дифференциального исчисления в норми- нормированных пространствах. Вторая глава посвящена линейному программированию. В ней вна- вначале даются постановки задач линейного программирования, правило решения задач в канонической форме по симплекс-методу, приводят- приводятся с решениями примеры. Вводится понятие двойственности, затем проводится строгое обоснование симплекс-метода, дается ряд методов нахождения первоначальной крайней точки. Полученные навыки при- применяются к некоторым наиболее известным типам задач линейного программирования - транспортным задачам и задачам о назначении. Основная цель при этом - ознакомление студентов с имеющимися методами решения задач линейного программирования и проведение обоснования этих методов. Обоснование проводится таким образом, чтобы для решения подобных задач в дальнейшем возможно было бы самостоятельно создать метод решения и провести его обоснование. В пособии приведены доказательства теоремы существования решений и теоремы двойственности, позволяющие более глубоко понять данный курс. Предисловие 5 В третьей главе приводятся следующие элементарные задачи класси- классического вариационного исчисления: простейшая задача, задача Больца. изопериметрическая задача. Все эти задачи являются частным случаем более общей задачи Лагранжа. Как частный случай задачи Лагранжа рассматриваются задача с подвижными концами и задача со старшими производными. В четвертой главе рассматриваются задачи оптимального управле- управления. Приводится формулировка и доказательство принципа максимума Понтрягина в общем случае, а также принципа максимума для задачи со свободным концом. Решаются простейшая задача о быстродействии, задача Ньютона и ряд других задач оптимального управления. В пятой главе даны необходимые и достаточные условия экстремума в простейшей задаче классического вариационного исчисления. Глава 6, составляющая вторую часть, написана В.М.Тихомировым и посвящена обзору всей теории экстремальных задач с единых совре- современных позиций. Она основана на записях курса лекций, читавшегося Тихомировым В. М. на механико-математическом факультете МГУ осе- осенью 1998 года. В ней в сжатой форме выражено воззрение на теорию экстремальных задач, составившее стержень книг Иоффе А. Д., Тихо- Тихомиров В. М. «Теория экстремальных задач», М.: Наука, 1974 и Алексе- Алексеев В. М., Тихомиров В. М., Фомин С. В. «Оптимальное управление», М.: Наука, 1979. Эта часть рассчитана на преподавателей вузов и университетов (в особенности, на ведущих занятия по курсам оптимизации), студентов старших курсов университетов и научных работников, интересующихся проблемами теории экстремума и местом, которое занимает этот раздел анализа в современной математике. Глава 6 написана в надежде на то, что она поспособствует модернизации курсов оптимизации в будущем. Глава 6 состоит из пяти параграфов, посвященных принципу Лагран- Лагранжа для необходимых условий экстремума, возмущениям экстремальных задач, существованию решений, алгоритмам оптимизации. Отдельный пятый параграф посвящен решению конкретных задач. Э. М. Галеев, В. М. Тихомиров
Часть I Введение Теорию задач на отыскание наибольших и наименьших величин называют теорией экстремальных задач. Слово maximum по латыни означает «наибольшее», слово minimum - «наименьшее». Оба этих понятия объединяются словом «экстремум» (от латинского extremum, означающего «крайнее»). Слово «экстремум», как термин, объединяющий понятия «максимум» и «минимум», ввел в употребление Дюбуа-Реймон. Ныне раздел анализа, в котором изучают разнообразные задачи на максимум и минимум, называют теорией экстремальных задач. Запись задачи в виде /(х) -» extr означает, что мы должны решить и задачу на минимум, и задачу на максимум. Задачу на максимум всегда можно свести к задаче на минимум, заменив задачу f(x) -> max задачей f(x) -> min, где f(x) = -f(x), и наоборот. Поэтому в тех случаях, когда формулировки теорем для задач на минимум и максимум различны, мы иногда будем ограничиваться рассмотрением задачи на минимум. Задачи на максимум и минимум изначально формулируются, как правило, на языке той области, в которой они возникают. А исследуют их средствами математического анализа. Для того, чтобы можно было воспользоваться этими средствами, необходимо перевести формулировку задачи на язык математического анализа. Такой перевод называется формализацией. В общем виде формализованная задача выглядит следующим обра- образом: найти экстремум (максимум или минимум) функции f:X -> R, определенной на некотором пространстве X при ограничении х € D (D С X). Кратко записываем так: f(x) - extr; x € D. (Р) Для функции одной переменной X = R, для функции нескольких переменных X = R". В более общих случаях X может быть линей- линейным, нормированным или топологическим пространством. Ограничение х € D может быть записано в виде включения, а также в виде уравнений или неравенств. (Р) - нумерация (обозначение) задачи (от английского слова problem - задача). Множество допустимых элементов в задаче (Р) обозначаем D = D(P) или DP. Если множество допустимых элементов Введение 7 совпадает со всем пространством (?> = X), то задачу (Р) называем задачей без ограничений. Решением задачи (Р) на минимум является точка х такая, что f(x) ^ /(х) для всех точек х 6 D(P). В этом случае мы пишем х е absminP. Такой минимум называется еще абсолютным, или гло- глобальным. Аналогично определяется абсолютный максимум в задаче (absmaxP). Величина /(г), где х - решение задачи, называется чи- численным значением задачи и обозначается 5min или Smax (иногда, чтобы подчеркнуть глобальность экстремума, 5absmin или Sabsmax). Множество решений задачи (Р) обозначается АщР. Если экстремум не достигается, то мы должны указать последовательность точек хп, на которой значение функции f(xn) стремится к величинам 5mjn и 5так. При решении задачи следует отыскать не только абсолютные (гло- (глобальные) экстремумы задачи, но и локальные экстремумы. Точка х является точкой локального минимума в задаче (Р) (пишем х € locminP), если существует окрестность U точки х такая, что f(x) ^ f(x) для любой допустимой точки х из этой окрестности (V х € D П U). Аналогично точка х является точкой локального максимума в задаче (Р) (пишем х 6 locmaxP), если существует окрестность U точки х такая, что f(x) ^ /(х) V х € D П U. Если речь идет о максимуме или минимуме, то пишем locextrP. В связи с каждой экстремальной задачей возникают вопросы: ка- каковы необходимые условия экстремума, каковы достаточные условия, существует ли решение задачи, как найти решение явно или численно. В теории экстремальных задач наиболее разработаны необходимые условия, которым должно удовлетворять решение задачи. Выписывая эти необходимые условия экстремума, мы находим некоторое множество то- точек, удовлетворяющее этим условиям. Это множество точек (мы называем их стационарными, или критическими, или экстремальными), возможно, шире, чем множество абсолютных и даже локальных экстремумов. По- Поэтому далее надо с каждой такой точкой разобраться, доставляет она экс- экстремум (и какой) или нет. Это делается с помощью достаточных условий. Одним из важнейших принципов решения задач с ограничениями является принцип Лагранжа снятия ограничений. Ниже он будет сфор- сформулирован и доказан для некоторых конкретных типов задач. Сфера применимости принципа Лагранжа достаточно широка. Иногда нельзя к задаче применить имеющуюся теорему, однако этот принцип, приме- примененный без обоснования, тем не менее может привести к точкам, среди которых можно выделить решение.
Глава 1 Экстремальные задачи § 1. Конечномерные задачи без ограничений В этом параграфе даются необходимые и достаточные условия экстремума функций одной и нескольких переменных. 1.1. Постановка задачи Пусть /: R" -» R - функция п действительных переменных, облада- обладающая некоторой гладкостью. Под гладкостью мы понимаем определен- определенную дифференцируемость функции. Если функция / дифференцируема к раз в точке х, мы пишем / G ?>*(;?). Гладкой конечномерной экстре- экстремальной задачей без ограничений называется следующая задача: j \Xf > extr. При решении задачи надо найти отыскать не только абсолютные (гло- (глобальные) экстремумы (минимумы и максимумы) функции, но и локаль- локальные экстремумы. Точка х является точкой локального минимума (максимума) функ- функции /, если существует окрестность Ue = [х \\х-х\ < е} точки х такая, что fix) ^ /(х) (/(х) < fix)) для любой точки х из этой окрестности. При этом мы пишем х? locmin/ (ж 6 locmax/), а если речь идет о минимуме или максимуме, то пишем х € locextr/. 1.2. Необходимые и достаточные условия экстремума 1.2.1. Функции одной переменной Теорема 1 (Ферма). Пусть /: R -¦ R - функция одного действи- действительного переменного. Если х б locextr / - точка локального экстремума функции f и / € Dix) дифференцируема в точке х, то fix) = 0. § 1. Конечномерные задачи без ограничений 9 Доказательство. По определению дифференцируемое™ /(х + ft) = j(x) + f"(x)h + r(h), r(h) - o(h) = o(l)ft при малых ft. Значит, f(x + h)- f(x) =(/"(*) +o(l))ft. Если бы /"(*) ф 0, то при h достаточно близких к нулю, величина /"(х)+оA) имела бы знак /"(х), поскольку о(\) -> 0 при h -» 0. Само же h может принимать как положительные, так и отрицательные значения. Следовательно, разность f(x + h) - f(x) может быть как меньше, так и больше нуля. Это противоречит тому, что f(x + h) - f(x) ^ 0 при х? locmin/ и /(? + h) - f(x) 4 0 при х € locmax/. ¦ Геометрически теорема Ферма утверждает, что в точке экстремума дифференцируемой функции касательная к ее графику горизонтальна. Теорема 2. Пусть функция / € D2(x) дважды дифференцируема в точке it. Необходимые условия экстремума: если х е locmin / - точка локаль- локального минимума функции /, то /"(*) = 0, /"(*) ^ 0. Достаточные условия экстремума: если /"(*) = 0, /"(*) > 0, то х g locmin / - точка локального минимума функции /. Доказательство. По формуле Тейлора f"(x)h+]-f"(x)h2 r(h) = o(h2). Необходимость. Пусть х € locmin/. Тогда, во-первых, по необходи- необходимому условию экстремума I порядка для функций одной переменной - теореме Ферма - /"(х) = 0, во-вторых, /(х + h) - /(*) > 0 при достаточно малых h. Поэтому в силу формулы Тейлора /(х + h) - f(x) = l- 0 (r(ft) = o(h2)) при малых ft. Разделим обе части последнего неравенства на Л2 и устре- устремим h к нулю. Поскольку -^ > 0, то получим, что f"(x) ^ О.- Достаточность. Пусть /"(х) = 0, /"(х) > 0. Тогда по формуле 2 2 Тейлора в силу условия r(ft) - o(h2) «¦ |r(ft)| любого е > 0 при достаточно малых ft имеем: eft /(x + ft)-/(z)=-/"(x)ft2 + r(h) => r(ft) - e)ft2 -eh2 для При Е /"(*) . Следовательно, x € locmin /.
10 Глава 1. Экстремальные задачи Для локального максимума неравенства имеют противоположный вид: f"(x) ^ 0 и f"(x) < 0 соответственно. В одномерном случае можно дать почти исчерпывающий ответ на вопрос о том, является ли данная точка? локальным экстремумом или нет. Теорема 3. Пусть функция / e Dn(x) n раз дифференцируема в точке х. Необходимые условия экстремума: если х G locmin (max) / - точка локального минимума (максимума) функции /, то либо f"(x) = = f(n)(x) - 0, либо /"(*) = ... =/Bт-|)(х) = 0, *->(*) >0 (fi2m)(x) < 0) (I) при некотором т: 2 < 2т ^ п. Достаточные условия экстремума: если выполняется условие (I), то х 6 locmin (max) / - точка локального минимума (максимума) функции /. Доказательство. Пусть для определенности х е locmin/. По фор- формуле Тейлора, r(ft) = o(ft") при Л Необходимость при и = I следует из теоремы Ферма. Пусть далее п> 1. Тогда либо f"(x) = ... = f{n)(x) = 0, либо f"(x) = ... - /<"-">(?) = 0, /<">(*) ф 0, I < п. Значит, ^ Поскольку ж е locmin/, то /(i + Л) - f(x) = ^ hl + r,(h) > 0 при достаточно малых по модулю h. Так как /*"*(?) ф 0, то отсюда следует, что i - четно и /(/)(ж) > 0. Достаточность. Пусть /"(ж) = ... = fBm~^(x) = 0, f2m(x) ф 0. Тогда по формуле Тейлора Bт)! приЛ-0. Поскольку /Bш)(*) > 0, то f(x + Л) - /(г) ^ 0 при достаточно малых Л, т. е. х? locmin/. ш § 1. Конечномерные задачи без ограничений 11 1.2.2. Функции нескольких переменных Сформулируем необходимое условие экстремума I порядка в конеч- конечномерной задаче без ограничений, являющееся аналогом теоремы Ферма. Теорема 1. Если х = (хи...,х„) е locextr/ - точка локального экстремума функции п переменных f(x\,...,xn) и функция f 6 D(x) дифференцируема в точке х, то /"(*) = 0 д/(х) df(x) = 0. дх\ дхп Доказательство. Рассмотрим функцию одной переменной <р(х{) = f(xx,...,Xi-\,Xi,xi+u...,xn). Поскольку х = (хи...,хп) 6 locextr/, то?i e locextr <р. Кроме того <р 6 D(x{). По необходимому условию экстремума для функций одной переменной - теореме Ферма Ь) = 0 = 0. Сформулируем необходимые и достаточные условие экстремума II порядка в конечномерной задаче без ограничений. Предварительно напомним, что второй производной функции нескольких переменных является симметричная матрица вторых производных ij=\ а также приведем определения знакоопределенностей симметричных матриц. Матрица А называется неотрицательно определенной (А ^ 0), если (Ah, ft) > 0 V h € R" 0 V ft = (ft,..., Л„) 6 Rn. Матрица А называется положительно определенной (А > 0), если (Ah,h)>0 VftGR", ft^O. Матрица А называется строго положительно определенной, если существует а > 0 такое, что (Ah,h) > a\\h\\2 V Л е R". Аналогично определяются неположительная и отрицательная матрицы. Отметим, что в конечномерном пространстве условие положительной определенности симметричной матрицы А эквивалентно условию стро- строгой положительности матрицы А. В бесконечномерных пространствах это не так (см. [АТФ, с. 242|).
" 2 Глава 1. Экстремальные задачи Теорема 2. Пусть функция / 6 D2(x) дважды дифференцируема в точке А = (*,. ..,*„). Необходимые условия экстремума: если А € locmin(max)/ - точка локального минимума (максимума) функции /, то) > 0 ((f"(x)k, А) < 0) V Л е R". Достаточные условия экстремума: если /"(*) = 0, (/"(z)A,ft)>0 ((/"(*)Л,А)>0) VfteR", hjtO, то х? locmin (max) / - точка локального минимума (максимума) функ- функции /. Доказательство. По формуле Тейлора f(x + А) = /(*) + +r(h), r(h) = o(|ft|2). Докажем теорему для случая минимума. Случай максимума аналогичен. Необходимость. Поскольку х е locmin/, то, во-первых, по не- необходимому условию экстремума I порядка в конечномерной задаче без ограничений - аналогу теоремы Ферма f"(x) = 0, во-вторых, f(x + Aft) - f(x) ^ 0 при достаточно малых А. Поэтому в силу формулы Тейлора f(x + Aft) - f(x) = -(f"(±)h, ft) + r(Aft) ^ 0 (r(AA) = o(|A|2)) при малых А и фиксированном ft. Разделим обе части последнего неравенства на А2 и устремим А к нулю. Поскольку r(Xh)/X2 -> 0, то получим, что (f"(x)h,h)>o vfteR". Достаточность. Так как f"(x) = 0, то по формуле Тейлора в силу выполненного условия (f"(x)h,h) ^ а|А|2 имеем: Л) - f(x) = l-(f"(x)h, h) + r(h) > ||Л|2 + r(A) > 0 при достаточно малых Л, так как г(Л) = o(|ft|2). Следовательно, х б locmin/. я п Замечание. Для квадратичных функционалов Q(x) = ? aijXiXj условие положительной (отрицательной) определенности матрицы ^ - / (А) = (лу)^-=| является достаточным условием абсолютного ми- минимума (максимума) функционала. § 1. Конечномерные задачи без ограничений 13 1.2.3. Критерий Сильвестра Знакоопределенность матрицы устанавливается с помощью критерия Сильвестра. Напомним, что последовательными главными минорами матрицы А (аи ¦ ¦ <*it Главным минором А{{ ^ матрицы А называется определитель ма- матрицы размера k x к, составленной из строк и столбцов с номерами =det aiiik Теорема. . Пусть А - симметричная матрица. Тогда 1. Матрица А положительно определена (А > 0) тогда и только тогда, когда все ее последовательные главные миноры положительны, т. е. А\...к > 0, к - 1,... ,п. 2. Матрица А отрицательно определена (А < 0) тогда и только тогда, когда все ее последовательные главные миноры чередуют знак, начиная с отрицательного, т. е. (-l)*det А|...* > 0, k = 1,... ,п. 3. Матрица А неотрицательно определена (А ^ 0) тогда и только тогда, когда все ее главные миноры неотрицательны, т.е. Ail,.it ^ 0, 1 < »i <...<**< n, fc= 1,...,п. 4. Матрица А неположительно определена (А ^ 0) тогда и только тогда, когда все ее главные миноры чередуют знак, начиная с неположи- неположительного, т.е. (-I)*i4i,...jt ^0, 1 < ё| < ... ^ г* ^ п, к = 1,... ,п. Замечание 1. Как будет показано ниже, положительность (неотрица- (неотрицательность) матрицы равносильна положительности (неотрицательности) всех собственных значений матрицы. Замечание 2. Отметим, что условие положительности последователь- последовательных главных миноров матрицы равносильно условию положительности всех главных миноров (см. ). Для условия неотрицательности это не так, т. е. из условия неотрицательности последовательных главных миноров не следует неотрицательность всех главных миноров матрицы и, следовательно, не следует неотрицательность матрицы. Действительно, у матрицы А - (Q _. 1 последовательные главные миноры равны нулю (Ах = An = 0), но она не является неотрицательной: Dft, A) = <@,-A2),(Ai,A2)) = -h22 < 0 при ft2 Ф 0.
14 Глава 1. Экстремальные задачи 1.2.4. Метод Ньютона (метод касательных) Для того, чтобы решить задачу без ограничений нужно найти стационарные точки - решения уравнения f"(x) = 0. Для решения таких уравнений численным способом можно воспользоваться замечательным приемом, восходящим к Ньютону. Итак, пусть нам требуется решить уравнение F(x) = 0. A) Здесь F - дважды непрерывно дифференцируемая функция одной пере- переменной. Будем искать решение уравнения A) методом последовательных приближений. Если хк - приближенное значение корня, то точное значение корня x = xk + hk, B) где hk мало, и в силу дифференцируемости функции F 0 - F(x) = F(xk + ft») = F(xk) + &(xk)hk + o(hk). Пренебрегая слагаемым o(hk), находим, что hk = -F(xk)/F"(xk). Внеся эту поправку в формулу B), получим новое уточненное приближенное значение корня: хки -xk + hk. Таким образом, мы имеем следующее рекуррентное соотношение для нахождения последовательных приближений к нулю уравнения A): Хк+{ -Хк~ F{xk) C) Геометрически метод Ньютона эквивалентен замене дуги кри- кривой у = F(x) касательной, проведенной в некоторой точке кривой (см. рис. 1). Пусть для определенности нам надо найти корень уравнения A), находящийся на отрезке [а, Ь] и F(b)F"(b) > 0. Положим х0 = Ь. Проведем касательную к кривой у - F(x) в точке (b, F(b)) = (ж0, F(x0)). В качестве первого приближения х\ берется абсцисса точки пере- пересечения этой касательной с осью Ох. Через точку (a:b.F(xi)) снова проводим касательную, абсцисса точки пересечения которой дает второе приближение х2 корня х и т.д. (рис. 1). Очевидно, что уравнение касательной в точке {xk,F(xk)) есть у = F(xk) + F"(xk)(x - хк). Полагая в этом уравнении у - 0, х = хк+\, имеем формулу C) 0 = F(xk) + F"(xk)(xk+I - хк) <=> xk+l =xk- F{xk)/F"{xk). § 1. Конечномерные задачи без ограничений У В 15 Рис. 1. Заметим, что если в нашем случае положить Xq = а и, следовательно, F(xo)F"(xo) < 0, то, проведя касательную к кривой у = F(x) в точке (a,F(a)), мы получили бы точку Х\, лежащую вне отрезка [а, Ь], т.е. при этом выбор начального значения в методе Ньютона оказался бы неудачным. Таким образом, в данном случае правильным начальным приближением? является условие F(xq)F"(xq) > 0. Имеет место следующая Теорема. Пусть F € С2(,R), значения функции F(a) и F(b) при- принимают разные знаки (F(a)F(b) < 0), функция F монотонна на отрезке [а, Ь], F"(x)F"(x) Ф 0 V х G [а, Ь]. Тогда, исходя из начального приближе- приближения х0 € [о, Ъ], удовлетворяющего неравенству F(xo)F"(xo) > 0, можно вычислить по методу Ньютона единственный корень уравнения F(x) = 0 с любой степенью точности. Если производная F"(x) мало меняется на отрезке [а, Ь\ или вычи- вычисление F"(xk) слишком трудоемко, то в формуле C) можно положить F"(xk) - F"(x0) для всех значений к = 0,1,2,... : хк+\ =хк- F{xk)/F/(xti). Такой метод нахождения корня уравнения называется модифицированным методом Ньютона. Геометрически этот способ означает, что мы заме- заменяем касательные в точках (xk,F(xk)) прямыми параллельными первой касательной, построенной в точке (жо,.Р(а;о)). Подробнее о методе Ньютона можно прочитать в книге «Основы вычислительной математики» Б. П.Демидович и И. А. Марон .
16 Глава 1. Экстремальные задачи 1.3. Правило решения Для решения конечномерной задачи без ограничений следует: 1) Выписать необходимое условие экстремума I порядка - аналог теоремы Ферма: /"(ж) = О дх. дхп -/=o. Найти точки х, удовлетворяющие необходимому условию I порядка (эти точки называются стационарными). 2) Проверить выполнение условий экстремума II порядка в каждой стационарной точке. Выписать матрицу вторых производных A = a) Проверить выполнение достаточных условий экстремума - иссле- исследовать ее знакоопределенность, т.е. посчитать последовательные главные миноры матрицы А: A\...k = det ((ao-)*j=i), к = 1,... ,п. Если все ее они положительны, т.е. А\...* > 0, к = 1,...,п, то точка х доставляет локальный минимум в задаче, ж g locmin/. Если все ее последовательные главные миноры чередуют знак, начиная с отрицательного, т.е. (-l)*det.A|...» > 0, к = 1,... ,п, то точка доставляет локальный максимум, ж 6 locmax/. b) Если не выполняются достаточные условия экстремума, то надо проверить выполнение необходимых условий - исследовать ее слабую знакоопределенность, т. е. посчитать главные миноры матрицы А - определители матриц размера к х к, составленных из строк и столбцов с номерами, ...jt: = det aik Если матрица А не является неотрицательно определенной (А ^ 0), т. е. не выполняется условие, когда все ее главные миноры неотрица- неотрицательны, т. е. -A ,-,...,-t 0, 1 < ... ^ ik ^ п, к - 1,... ,та, то точка х не доставляет локальный минимум, ж? locmin/. Если матрица А не является неположительно определенной (А? 0), г. е. не выполняется условие, когда все ее главные миноры чередуют знак, начиная с неположительного, т.е. (-1)*_4,-,...,-4 > 0, 1 ^ i\ < ... < г* < п, к = 1,... ,п, то точка х не доставляет локальный максимум, ж ^ locmax/. § 1. Конечномерные задачи без ограничений 1.4. Примеры Пример 1. /(ж) = /(жьж2) = х\ - Ж|Ж2 +х\- 2ж| + ж2 -» extr. Необходимое условие экстремума I порядка: df(x) df(x) 17 /"(ж) - 0 = 0 (2ж, -ж2 -2 = 0; I -ж, +2ж2 + 1 = 0. дж, дх2 Решая эту систему, находим единственную стационарную точку ж = A,0). ! -1 Матрица вторых производных по кри- терию Сильвестра положительно определена. По достаточному усло- условию локального экстремума функции нескольких переменных точка A,0) € locmin/. Поскольку функционал является квадратичным, то A,0) е absmin/, a Smax = +оо. Пример 2. /(ж) = /(Ж1,Ж2) = х* + х\ - х\ - 2ж|Ж2 - х\ -» extr. Необходимое условие экстремума I порядка: /"(ж) = 0 а/(х) =.df(&) дх | дх2 = 0 4x1 ~ = 0. Решая эту систему уравнений, находим стационарные точки х = (ж(,ж2) = A,1), х2 = (-1,-1), ж3 = @,0). Для проверки условий II порядка выписываем матрицу вторых производных: /12*?-2 V 2 V -2 12*1- -2 *1 =Л Матрица A,1) 10 -2 (-1,-1) Ш2 702 ~2 10)" Ат-{-2 -г)- по критерию Сильвестра положительно опре- определена. По достаточному условию локального экстремума функции нескольких переменных точки A,1) и (-1,-1) доставляют локальный минимум функции /. Матрица по критерию Сильвестра не является ни поло- жительно, ни отрицательно определенной. Она является неположительно определенной матрицей (А ^ 0) и не является неотрицательно опреде- определенной матрицей (А ^ 0). Следовательно, не выполняется необходимое условие локального минимума. Поэтому ж3 - @,0) ? locmin/. Посколь- Поскольку f(h,-h) = 2ft4 > 0 = /(ж3) при малых h Ф 0, то ж3 ? locmax/. Очевидно, что Sm3X - +оо.
18 Глава 1. Экстремальные задачи Пример 3. Найти экстремумы неявно заданной функции двух пере- переменных х3 = f(xi,x2), если F(x, х2, X}) = х] + х\ + х\ - 2х\ + 2х2 - 4х2 - 10 = 0. = |^-. и ff - |^ находим Решение. Частные производные из уравнений: dF 8F dxj 2х,- 2 + Bх3 -4)^=0, ах dF dF (*) = 0, дх2 дх$ дх2 Необходимое условие экстремума I порядка: _ дхъ(х) _п- S± /24,-2 = 0,)^ дх2 = 0. Эх, дх2 _ / 12* 2 + 2 = /*¦ = !, U2 = -l- Подставляя найденную точку (х|,х2) = A, - 1) в заданное уравнение Р(х|,х2,хз) - 0, находим две стационарные точки х" = (х!,Х2,Хз) = A,-1,-2) и x2 = (Xl,x2,x2) = A,-1,6) Для проверки условий II порядка надо выписать матрицу вторых производных в каждой стационарной точке. Дифференцируя первое уравнение правой части системы уравнений (*) по х\ и Х2 с учетом 0X3 dxj условия = = 0, имеем oxi дх2 1 * J" 4" д2х. д2х3 дххдх2 дх1дх2 = 0. Аналогично, дифференцируя второе уравнение правой части системы (*) по Х[ и 12, получим д2хъ 2х2 д2х7 1 4" д2х7 1 4" Очевидно, что д2хъ д2хъ дх\дх. Таким образом, А = dxidx; I Л.,-. " v о = (~o7 § 1. Конечномерные задачи без ограничений 19 Матрица А\& по критерию Сильвестра является положительно определенной, а матрица А\& отрицательно определенной. Поэтому по достаточному условию второго порядка in = ~^> 5i ocmax = 6. Можно показать, что это будут не только локальные экстремумы, но и глобальные. Приведем несколько примеров различных свойств экстремумов в за- задаче без ограничений. Пример 4. Абсолютные минимумы и максимумы достигаются в беско- бесконечном числе точек: /: R -> R, /(х) = sin а;. Пример 5. Функция ограничена, абсолютный максимум достигается, минимум - нет: /: R - R, f{x) = 1 1+х2" Пример 6. Функция ограничена, но абсолютные максимум и минимум не достигаются: /:R-»R, /(x) = arctgx. Пример 7. Функция ограничена, имеет стационарные точки, но абсо- абсолютные максимум и минимум не достигаются: /:R->R, /(x) = (arctgxK. Пример 8. Функция ограничена, имеет локальные максимумы и мини- минимумы, но абсолютные максимум и минимум не достигаются: /: R-»R, /(х) = arctgx ¦ sinx. Пример 9. Ограничение функции, заданной на плоскости, на любую прямую, проходящую через начало координат, имеет в нуле локальный минимум, но вместе с тем начало координат не является точкой локального минимума: /: R2 -» R, /(х, х2) = - Зх2). " Действительно, на любой прямой Х\ - ах2, а € R, функция вида f(ax2,x2) = (ах2 - Х2)(«Х2 - За;^) = х\(а - х2)(а - Зх2) = х^а2- 4ах2 + Ъх\) ^ 0 = /@) при малых Х2. Значит, на любой прямой вида X! = ах2 функции / имеет локальный минимум в нуле. Аналогично на прямой Ж2 = 0 функция /(х|,0) = х2 имеет минимум в нуле. С другой стороны, на параболе х\ = 7х\ функция fGx\,x2) - -х2 < 0 в любой окрестности нуля. То есть точка х = 0 не является точкой локального минимума функции /.
20 Глава 1. Экстремальные задачи Пример 10. Имеется единственный локальный экстремум, не яв- являющийся абсолютным: /: R2 - R, f(Xl, х2) = х] - х\ + 2е~х*. Необходимое условие экстремума I порядка в конечномерной задаче без ограничений: /"(*) = 0 дх2 = 0 -2x2 = 0, -{ = 0; i, = 0, 2e~x" = 1 о -z2 = In | = - In 2 & xs - ±v1n2; x2 = 0. Получаем в задаче три стационарные точки х1 = @,0), х2 = {\Дп2,0), 43 = (-Ип2,0). Для проверки условий II" порядка надо выписать матрицу вторых производных в каждой стационарной точке: А = _ 2- 4е~х" "" Л) „.„=(» -2j^,. = 4..= (о2 Л) Матрица вторых производных I „"" \ } по кРитеРию Сильвестра является отрицательно определенной: А\ = -2 < 0, А2 = 4 > 0. Поэтому по достаточному условию второго порядка стационарная точка ж" g locmax. Очевидно, что Sabcmax - +оо (/(аг|,0) -» +оо при а;, -* +оо). 0 i 41п2 Матрица вторых производных J q по критерию Силь- Сильвестра не является ни положительно, ни отрицательно определенной и более того не является ни неположительно определенной матри- матрицей (A fC. 0) и ни неотрицательно определенной матрицей (А % 0). Следовательно, не выполняется необходимое условие ни локального максимума, ни локального минимума. Поэтому стационарные точки х2, ¦locextr/. Очевидно, что 5at,smax = +°°- Действительно, функция f(x[,0) = - 2е~х" -> +оо при а;| -> +оо. Значит, у функции / имеется единственный локальный экстремум в точке х = @,0), не являющийся абсолютным. г3 *? § I. Конечномерные задачи без ограничений 21 Пример 11. Можно ли утверждать, что если функция одной переменной имеет в какой либо точке локальный минимум, то в некоторой достаточно малой окрестности этой точки слева от точки функция убывает, а справа возрастает? Нет. Контрпример: /(*) = { ^ B + sin «) х ф °" [О, х = 0. Ясно, что х = 0 € absmin/. С другой стороны, в любой окрестности нуля и справа, и слева производная f"(x) - 2zB + sin -) - cos -, x ф 0, принимает как положительные, так и отрицательные значения, т.е. функция / и возрастает, и убывает. Пример 12. Имеется бесконечное число локальных максимумов, но нет ни одного локального минимума: /: R2 -» R, f(xux2) = sin ;r2 - х]. Необходимое условие экстремума I порядка: 8f(x) df(x) дх. дх2 = 0 -2яг, =0; cos x2 = 0, = i + kw, Jtez. Стационарные точки хк = @, | + кж), к е Z. Для проверки условий II порядка надо выписать матрицу вторых производных в каждой стационарной точке: А- (d2f(x)V =/_2 0 \ (O.f+2n,) ~2 @,f+Bn+l)*) _/-2 0\ Матрица (о2 -".) по критерию Сильвестра является отрицатель- отрицательно определенной: At - -2 < 0, А2 = 2 > 0. Поэтому по достаточному условию второго порядка @, | + 2птг) € locmax/ V n € Z. Матрица I „ . I по критерию Сильвестра не является неот- неотрицательно определенной матрицей (A J? 0). Следовательно, не вы- выполняется необходимое условие локального минимума. Поэтому точки @, | + Bп + 1)тг) не доставляют локального минимума. Точки локаль- локального минимума могли быть только среди стационарных точек, но там их не оказалось. Следовательно, нет ни одного локального минимума.
22 Глава 1. Экстремальные задачи 1.5. Задачи, упражнения В задачах 1.1-1.17 без ограничений найти стационарные точки, проверить их на экстремальность, а также найти все локальные и глобальные минимумы и максимумы. 50 20 1.1. f(xl,x2) = x,x1+ - + >extr. Х\ Х2 1.2. /(х,ж2) = х\-х\- 4ж, + 6х2 -» extr. 1.3. 1.4. - 16x, - 12a;2-+extr. x]-2x3^e 2х,ж3 + Зж2ж3 - ж, ->¦ extr. 1.5. f(xux2,Xi) = x\ + x\ + 2x\ 1.6. /(a;ba;2) = a;?+ar2-3xiX2^ 1.7. /(х,ж2) = Зж,ж2 - x\x2 - x\x\ -» extr. 1.8. f(xux2) = x\ +X2 - (ж, + ж2L -» extr. 1.9. /(жьж2) = 2act + «2 - «i - 2ar2 -» extr. 1.10. /(«1,^2) = Ж|Ж21п(ж? + Х2)-> extr. 1.11. /A1,12) = x\x\{6 - x, - x2) -> extr. 1.12. /(ж,х2) = e2zi+iX2(Sx2 - 6x{x2 + 3x22) -» extr. 1.13. f(xi,x2) = ех"~Х2E - 2x, +x2) -» extr. 1.14. f(xux2,x3) = xixlxlG - Xi - 2x2 - Ъхъ) -» extr 1 1.15. f(xux2)= [{ -1 mm (задача о полиномах Лежандра второй степени). 1.16. (задача о полиномах Лежандра третьей степени). 1.17. Найти экстремумы неявно заданной функции двух переменных хъ = f(x\,x2), если 2a;i + 2ж2 + 2х3 - 2 = 0. § 2. Конечномерные гладкие задачи с равенствами 23 § 2. Конечномерные гладкие задачи с равенствами В этом параграфе даются необходимые и достаточные условия экстремума в гладкой конечномерной задаче с ограничениями типа равенств. 2.1. Постановка задачи Пусть /,: R" -» R, г - 0,1,... ,т, - функции п переменных. Считаем, что все функции ft обладают определенной гладкостью. Гладкой конечномерной экстремальной задачей с ограничениями типа равенств называется следующая задача: /о(ж) -* extr; /,(ж) = 0, i = 1,..., т. (Р) 2.2. Необходимые и достаточные условия экстремума 2.2.1. Принцип Лагранжа Сформулируем необходимое условие экстремума I порядка в гладкой конечномерной задаче с ограничениями типа равенств - принцип Лагранжа. Теорема. Пусть х € locextrP - точка локального экстремума в за- задаче (Р), а функции ft, г = 0,1,...,т, непрерывно дифференцируемы в окрестности точки ж (условие гладкости). Тогда существует ненулевой вектор множителей Лагранжа А = (Ао, А|,..., Am) Е Rm+I, А Ф 0, такой, т что для функции Лагранжа задачи (Р) А(ж,А) = условие стационарности выполняется >=о дЛ(ж, А) = 0, i= >=0 Это соотношение называется условием стационарности. Точки, удо- удовлетворяющие условию стационарности, называются стационарными. Доказательство проведем от противного. Предположим, что условие стационарности не выполняется. Это означает, что векторы /,"(х) = fdfAx) dfi(x)\ I ,- -, I, » = 0, l,...,ra, линейно независимы. Поэтому \ 9xi дх„) 3/о(х) dfo(x) \ ранг матрицы А /dfi(x)\ - (- 1 = V dxj) ".=°.-.m дхх \ дх, дх„ dfm"(&) дхп равен
24 Глава 1. Экстремальные задачи тп + 1. Тогда по теореме о ранге матрицы (см. {13, с. 71]) существует матрица М порядка (т + 1) х (т + 1) с определителем, отличным от нуля. Допустим для определенности, что этой матрицей является матрица, составленная из первых столбцов матрицы А: det (\ Ofm(x) \ dfm(&) dx m+l He ограничивая общности, считаем, что fo(x) = 0. Действительно, если fo(?) Ф 0, то следует рассмотреть функцию fo(x) = fo(x) - fo(x) и для нее будет fo(x) = 0. Положим F(x) = (F0(x),..., Fm(x)) - (fo(x,xm+2,... ,xn),...,fm(x,xm+2,-¦¦¦,?„)) для вектора х = (xu..., xm+i). Функция F отображает некоторую окрестность точки х - (хи... ,?т+\) 6 Rm+1 в Rm+I, и является (в силу условий гладкости теоремы) непрерывно дифференцируемым отображением в этой окрест- окрестности, F(x) = 0. Кроме того, якобиан отображения F в точке х отличен от нуля, т.е. det (V = detM фО. По теореме об обратной функции в конечномерных пространствах (см. следующий пункт) существует обратное отображение F~* некоторой ок- окрестности точки у = 0 в окрестность точки х такое, что F~[(y = 0) = х и \F~\y) - \F"{(y)\ ^ К\у - 01 *> \F-\y) - х\ <: К\у\ с некоторой константой К > 0. В частности, для достаточно малого по модулю е определен вектор х(е):= F""(e,0,... ,0), для которого \х(е) - х\ ^ К\е\. Это означает, что F(x(e)) = (е,0, ...,0), что равносильно равенствам fo(x(e),xm+2,... ,хп) = е, /{(х(е),хт+2,... ,хп) = 0, i = 1,... ,m. Таким образом, для вектора х(е) = (х\(е),... ,xm+l(e),xm+2,... ,хп) выполня- выполняются условия fo(x(?)) = e, fi(x(e)) = 0,i=l,...,m, A) и при этом \х(е) - х\ < К\г\. B) Из соотношений A)-B) следует, что вектор х не доставляет в задаче экстремума, ибо вблизи его существуют допустимые векторы х(е), на которых функционал /о принимает значения как большие так и меньшие чем fu(x) (напомним, что fo(x) = 0). Получили противоречие с тем, что х G locextr P. Таким образом, наше предположение (противного) неверно и тем самым теорема доказана. ¦ § 2. Конечномерные гладкие задачи с равенствами 2.2.2. Конечномерная теорема об обратной функции. Теорема Венерштрасса 25 Теорема (конечномерная теорема об обратной функции). Пусть F: U -» R" - непрерывно дифференцируемое отображение некоторой окрестности U С R" точки х в R", F(x) = у и якобиан отображения F в точке? отличен от нуля (det F"(x) = det I I Ф 0 I. Тогда \ V dxj /i,j=\ > существует обратное отображение F~x некоторой окрестности V точки у в окрестность точки х такое, что F~"(j/) - x и с некоторой константой К > 0. Пусть /: R" -» R - функция п переменных. При исследовании вопроса о достижении функцией п переменных экстремума часто ис- используется следующая теорема. Теорема Вейерштрасса. Непрерывная функция на непу- непустом ограниченном замкнутом подмножестве конечномерного пространства (компакте) достигает своих абсолютных максимума и минимума. Выделим простое следствие из этой теоремы, которое часто будем использовать. Следствие. Если функция f непрерывна на R" и lim f(x) = +оо |х|-оо (lim f(x) = -oo), то она достигает своего абсолютного минимума |l|-со (максимума) на любом замкнутом подмножестве из R". Напомним, что множество А в метрическом пространстве назы- называется компактом, если из всякой последовательности- элементов А можно выбрать сходящуюся к элементу из А подпоследовательность или (равносильное определение) если из всякого покрытия А открытыми множествами можно выбрать конечное подпокрытие. Ограниченное и замкнутое множество конечномерного пространства является компактом. 2.2.3. Необходимое условие экстремума II порядка Сформулируем необходимое условие минимума II порядка в гладкой конечномерной задаче с ограничениями типа равенств.
26 Глава 1. Экстремальные задачи Теорема. Пусть х € locmin P - тонка локального минимума в зада- задаче (Р), функции fi, t = О, l,...,m, дважды непрерывно дифференцируемы в окрестности точки х (условие гладкости), dimlin*{/|(x),...,/^(i)} =n (условие регулярности). Тогда существует множитель Лагранжа А = A,А|,...,Ага) ? Rm+I такой, что для функции Лагранжа задачи (Р) ГЦ А(х, А) = /о(х) + выполняются условия стационарности: Л,D, А) = 0 и неотрицательности: {Axx(x,\)h,h)>0 V h: {/1(х), h)= О, г=\,...,т. Мы сформулировали необходимое условие минимума. Необходимое условие максимума формулируется аналогично, за исключением того, что множитель Лагранжа А = (-1, А,..., Am) G Rm+I и соответственно m функция Лагранжа А(х, А) = -fo(x) + ? А,/,(а;). i=i 2.2.4. Достаточное условие экстремума II порядка Сформулируем достаточное условие минимума II порядка в гладкой конечномерной задаче с ограничениями типа равенств. Теорема. Пусть функции f{, г = О, 1,... ,т, дважды непрерывно диф- дифференцируемы в окрестности точки х (условие гладкости), dim I in {/[(?), , /m(?)} = п (условие регулярности). Существует множитель Лагран- Лагранжа А = A, А|,..., Am) € Rm+I такой, что для функции Лагранжа задачи т (Р) А(х, А) = fo(x) + Y^, Ai/,(x) выполняются условия стационарности: Ах(х,А) = 0 и положительности: (Axx(x,X)h,h)>0 V/i5*0:
 Название:
Название:
Галеев Е. М., Тихомиров В. М.
Год:
2000
Жанр:
Учебное пособие
Издательство:
Едиториал УРСС
ISBN:
5-8360-0041-7
Язык:
Русский
Формат:
DjVu
Размер:
4 MB
Описание:
Книга посвяшена важнейшим проблемам оптимизации. Она построена на базе преподавания теории оптимизации на механико-математическом факультете МГУ. В основе ее лежат курсы, прочитанные и 1998/99 годах Э. М. Галееиым (Главы 1-5) и В. М. Тихомировым (Глава 6). Рассматриваются фрагменты следующих разделов теории экстремальных задач: линейного и выпуклого программирования, математического программирования, классического вариационного исчисления и оптимального управления. Приводятся как необходимые, так и достаточные условия экстремума. Для изучения этих разделов в необходимом объеме даются элементы функционального и выпуклого анализа. В каждом параграфе после теоретической части приводятся примеры решения задач, предлагаются задачи для решения на семинарах, контрольных и для домашних задании. Дается обзор общих методов теории экстремума.
Загрузить:
turbobit.net ifolder.ru depositfiles.com
 Название:
Оптимизация: Теория, примеры, задачи
Название:
Оптимизация: Теория, примеры, задачи
Галеев Е. М.
Год:
2002
Жанр:
Учебное пособие
Издательство:
Едиториал УРСС
ISBN:
5-354-00204-4
Язык:
Русский
Формат:
DjVu
Размер:
3 MB
Описание:
Книга посвящена важнейшим проблемам оптимизации. Она построена на базе преподавания теории оптамизации на механико-математическом факультете МГУ. В основе ее лежат курсы и спецкурсы, прочитанные Э. М. Галеевым. Рассматриваются фрагменты следующих разделов теории экстремальных задач: линейного и выпуклого программирования, математического программирования, классического вариационного исчисления и оптимального управления.
Приводятся как необходимые, так и достаточные условия экстремума. Для изучения этих разделов в необходимом объеме даются элементы функционального и выпуклого анализа. В каждом параграфе после теоретической части приводятся примеры решения задач, предлагаются задачи для решения на семинарах, контрольных и для домашних заданий. Дается обзор общих методов теории экстремума.
Для студентов вузов по специальностям «Математика», «Прикладная математика», а также для аспирантов, преподавателей и научных работников.
Загрузить:
turbobit.net ifolder.ru depositfiles.com
 Название:
Сборник задач по оптимизации. Теория. Примеры. Задачи
Название:
Сборник задач по оптимизации. Теория. Примеры. Задачи
Алексеев В. М., Галеев Е. М., Тихомиров В. М.
Год:
2005
Жанр:
Уч.пособие
Издательство:
ФИЗМАТЛИТ
ISBN:
5-9221-0590-6
Язык:
Русский
Формат:
DjVu
Размер:
2 MB
Описание:
В книге собрано примерно 700 задач на отыскание экстремумов для конечномерного случая, для задач классического вариационного исчисления,
оптимального управления и выпуклого программирования. Содержатся элементы функционального анализа, дифференциального исчисления и выпуклого анализа.
В книге приведены теория, необходимая для решения задач, и примеры. Основу решения всех задач составляет единый принцип, восходящий к Лагранжу. Часть задач приведена с решениями. Имеется большое количество трудных задач, которые могут быть использованы в качестве курсовых и дипломных работ.
Для студентов вузов по специальностям «Математика» и «Прикладная математика», а также для аспирантов и научных работников.