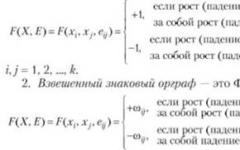Пусть G(V,X) – псевдограф и пусть вершины v и w (v¹w) данного графа можно соединить маршрутом. Тогда обязательно существует и минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута d(v, w). Положим также d(v, v) =0 для любой вершины vÎV; d(v, w) = ¥, если не существует маршрута, соединяющего v и w.
Определенная таким образом величина d(v,w) для любых вершин v и w графа G(V, X) называется расстоянием между v и w.
Число расстояний в графе с n вершинами равно числу сочетаний C n 2 .
Пусть граф G(V,X) связный. Определим для него следующие понятия:
Диаметр графа : d(G) = maxd(v, w).
Эксцентриситет (максимальное удаление) вершины : r(v) = maxd(v, w);
Радиус графа: r(G) = min r(v);
Центр графа : любая вершина vÎV,такая, что r(v) = r(G).
Диаметр графа, эксцентриситеты вершин, радиус графа и центры графа называются метрическими характеристиками графа.
Пример. Найти метрические характеристики графа, заданного диаграммой:
Найдем все расстояния, учитывая, что d(v, w) = d(w, v).
Число расстояний в данном графе С 5 2 = 5!/3!2! = 10: d(v 1 , v 2) =1, d(v 1 , v 3) = 2, d(v 1 , v 4) = 2, d(v 1 , v 5) = 3, d(v 2 , v 3) = 1, d(v 2 , v 4) = 1, d(v 2 , v 5) = 2, d(v 3 , v 4) = 1, d(v 3 , v 5) = 2, d(v 4 , v 5) = 1.
Диаметр графа d(G) =3.
Эксцентриситеты вершин: r(v 1) = 3, r(v 2) = 2, r(v 3) = 2, r(v 4) = 2, r(v 5) = 3.
Радиус графа r(G) = 2.
Центры графа v 2 , v 3 , v 4 .
3. Минимальные маршруты в нагруженных графах
Граф G(V, X) называется нагруженным, если на множестве ребер графа задана функция, называемая весовой, которая ставит в соответствие каждому ребру х ÎХ графа некоторое число l(x). Значение l(x) называется длиной дуги.
Величине l(x) можно придать разный смысл: затраты на транспортировку, время проезда, расстояние между пунктами, расход бензина и т.д.
Сумма длин ребер, входящих в маршрут, называется длиной маршрута.
Заметим, что если для всех х Î Х l(x) = 1, то граф можно рассматривать как ненагруженный.
Маршрут в графе G(V, X) из вершины v в вершину w (v¹w), называется минимальным, если он имеет минимальную длину среди всех маршрутов в графе G(V, X) из вершины v в вершину w.
Ограничимся графами, для которых l(x)>0.
При поиске минимального маршрута в нагруженном графе с l(x)>0
воспользуемся таким же утверждением, что и для ненагруженного графа, а именно:
любой минимальный маршрут является простой цепью.
Рассмотрим теперь задачу поиска минимального маршрута в нагруженном графе.
Пусть граф G(V,X) нагруженный, число вершин n ³ 2, необходимо построить минимальный маршрут из v 1 в v n .
Приведем алгоритм.
Шаг 1. Каждой вершине присвоить индекс a(v i): a(v 1) = 0, a(v i) = ¥, i ¹ 1. окрасить вершину v 1 и положить v = v 1 .
Шаг 2. Для каждой неокрашенной вершины v j изменить индекс по правилу:
a(v j) = min {a(v j), a(v) + l(v, v j)}.
Окрасить ту из вершин, для которой a(v j) окажется наименьшим.. окрасить также ребро, ведущее в выбранную на данном шаге вершину v j . Положить v = v j .
Шаг 3. Если v = v j , закончить процедуру, так как кратчайший маршрут из v 1 в v n . если v ¹ v n , то перейти к шагу 2.
Замечание. Шаг 2 невозможен, если все a(v j)= ¥. В этом случае вершина v n недостижима.
Применим изложенный алгоритм к заданному диаграммой графу. Найдем в нем кратчайший маршрут из v 1 в v 6 .

Шаг 1. Окрасим вершину v 1 . Присвоим вершинам индексы: a(v 1) =0, a(v 2) = a(v 3)=…= a(v n)=¥. Полагаем v 1 = v.
a(v 2) = min {¥, 0+4} = 4,
a(v 3) = min {¥, 0+7} = 7,
a(v 4) = min {¥, 0+3} = 3,
a(v 5) = min {¥, 0+¥} = ¥,
a(v 6) = min {¥, 0+¥} = ¥.
Окрашиваем вершину v 4 и ребро {v 1 , v 4 }.
Шаг 3. Так как вершина v 6 не окрашена, выполняем шаг 2, полагая v = v 4 .
a(v 2) = min {4, 3+¥} = 4,
a(v 3) = min {7, 3+¥} = 7,
a(v 5) = min {¥, 3+3} = 6,
a(v 6) = min {¥, 3+¥} = ¥.
Окрашиваем вершину v 2 и ребро {v 1 , v 2 }.
Шаг 3. Так как вершина v 6 не окрашена, выполняем шаг 2, полагая v = v 2 .
a(v 3) = min {7, 4+3} = 7,
a(v 5) = min {6, 4+2} = 6,
a(v 6) = min {¥, 4+¥} = ¥.
Окрашиваем вершину v 5 и ребро {v 4 , v 5 }.
Шаг 3. Так как вершина v 6 не окрашена, выполняем шаг 2, полагая v = v 5 .
a(v 3) = min {7, 6+¥} = 7,
a(v 6) = min {¥, 6+2} = 8.
Окрашиваем вершину v 3 и ребро {v 1 , v 3 }.
Шаг 3. Так как вершина v 6 не окрашена, выполняем шаг 2, полагая v = v 3 .
a(v 6) = min {8, 7+2} = 8.
Окрашиваем вершину v 6 и ребро {v 5 , v 6 }.
Так как вершина v 6 окрашена, то работу прекращаем. Получили минимальный маршрут v 1 v 4 v 5 v 6 , длина которого равна 8 .
Заметим, что это в данном случае не единственный для вершин v 1 и v 6 минимальный маршрут, т.к. в алгоритме имелась возможность окрасить вместо ребра {v 4 , v 5 } ребро {v 2 , v 5 }, тогда бы получили другой маршрут той же длины.
4. Задачи на деревьях
Ациклическим называется граф, в котором отсутствуют циклы.
Граф без циклов называется лесом.
Дерево – это связный ациклический граф.

Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w . Это расстояние удовлетворяет аксиомам метрики:
1) d(v, w) 0, причем d(v, w) = 0 тогда и только тогда, когда v= w;
2) d(v, w) = d(w, v);
3) d(v, w) d(v, u) + d(u, w).
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Пример 82.
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.

Рис. 3.16. Граф для примера 82
Решение.
Чтобы определить центры, радиус, диаметр графа G
, найдем матрицу D(G)
расстояний между вершинами графа, элементами d ij
которой будут расстояния между вершинами v i
и v j
. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G)
симметрична относительно главной диагонали. 
С помощью полученной матрицы для каждой вершины графа G
определим наибольшее удаление из выражения: ![]() для i,
j = 1, 2, …, 5
. В результате получаем: r(v 1) = 3,
r(v 2) = 2,
r(v 3) = 2,
r(v 4) = 2,
r(v 5) = 3.
Минимальное из полученных чисел является радиусом графа G
, максимальное – диаметром графа G
. Значит, R(G) = 2
и D(G) = 3
, центрами являются вершины v 2 ,
v 3 ,
v 4
.
для i,
j = 1, 2, …, 5
. В результате получаем: r(v 1) = 3,
r(v 2) = 2,
r(v 3) = 2,
r(v 4) = 2,
r(v 5) = 3.
Минимальное из полученных чисел является радиусом графа G
, максимальное – диаметром графа G
. Значит, R(G) = 2
и D(G) = 3
, центрами являются вершины v 2 ,
v 3 ,
v 4
.
В математике сети дорог (автомобильных и не только) представляются взвешенным графом. Населенные пункты (или перекрестки) - это вершины графа, ребра - дороги, веса ребер - расстояния по этим дорогам.
Для взвешенных графов предлагается множество алгоритмов. Например, популярный алгоритм Дейкстры для поиска кратчайшего пути от одной вершины до другой. У всех этих алгоритмов есть общая принципиальная (для математики) особенность - они универсальны, т.е. могут успешно применяться для графов любой конструкции. В частности, для каждого алгоритма известна его сложность – она примерно соответствует увеличению времени выполнения алгоритма в зависимости от числа вершин графа. Все это подробно можно прочитать, например, в википедии.
Вернемся к практическим задачам. Дороги представляются взвешенным графом, но дороги - это не любой граф. Другими словами, нельзя из любого графа построить дорожную сеть. В отличие от виртуального графа как математической абстракции, дороги строятся людьми из реальных материалов и стоят довольно больших денег. Поэтому они прокладываются не как попало, а по определенным экономическим и практическим правилам.
Мы не знаем эти правила, однако, работая с дорожными сетями, вполне можно использовать алгоритмы, которые эффективны для графов дорог, хотя и не подходят для графов в универсальном или математическом смысле. Рассмотрим здесь два таких алгоритма.
Несколько важных понятий и условностей
1. Мы будем использовать взвешенные неориентированные графы с неотрицательными весами ребер. В частности, дороги в рамках региона (страны) представляют собой именно такой граф.2. Матрица кратчайших расстояний (МКР) – ее маленький и простой пример можно найти во многих дорожных атласах. Эта табличка обычно называется примерно так: «расстояния между наиболее важными городами». Она выглядит как часть матрицы ниже или выше главной диагонали (из верхнего левого в нижний правый угол), потому что с другой стороны главной диагонали точно такие же цифры, другими словами элемент М(i,j)= М(j,i). Это происходит, потому что граф, как говорят математики, неориентированный. Строки и столбцы соответствуют городам (вершинам графа). В реальности такая таблица намного больше, так как в вершины графа, кроме городов, входят все деревни и перекрестки, но напечатать такую большую таблицу в атласе, естественно, невозможно.
Первым делом продолжим (мысленно) нашу таблицу на верхнюю часть, получим МКР, симметричную относительно главной диагонали и далее будем иметь в виду именно такую таблицу. В этом случае, столбец с некоторым номером равен строке с таким же номером и все равно, какое из понятий использовать. Мы используем и то, и другое, чтобы их пересекать между собой.
Наша МКР может быть: а) известна заранее, потому что мы ее подсчитали одним из методов поиска МКР; б) мы можем не знать МКР, а определять ее построчно по мере необходимости. Построчно – это значит, что для требуемой строки рассчитываются расстояния только от соответствующей ей вершины до остальных вершин, например, методом Дейкстры.
3. Еще пара понятий. Эксцентриситет данной вершины – это расстояние от этой вершины до самой удаленной от нее. Радиус графа – это наименьший из эксцентриситетов всех вершин. Центр графа – вершина, эксцентриситет которой равен радиусу.
Как это выглядит на практике. Центр дорожной сети – это город или перекресток, наименее удаленный от всех остальных пунктов этой сети. Радиус – максимальное расстояние от этого центрального узла до самого удаленного.
4. Степень вершины – количество ребер, которое присоединено к вершине.
У графов дорожных сетей, средняя степень всех вершин находится в районе от 2 до 4. Это вполне естественно – сложно и дорого строить перекрестки с большим количеством примыкающих дорог, не менее сложно потом пользоваться такой дорожной сетью. Графы, с невысокой средней степенью вершин называются разреженными, как видим, графы дорожных сетей именно такие.
Задача 1. Поиск радиус и центра графа по матрице кратчайших расстояний
Заметим, что у графа может быть несколько центров, но мы хотим найти любой из них.Как задача решается в общем случае? Полным просмотром МКР. Ищется максимальный элемент в строке (эксцентриситет каждой вершины), а потом из этих максимальных элементов находится минимальный.
Это далеко не самый быстрый способ. Для чего нужно быстрее, если, казалось бы, радиус и центр графа можно найти один раз? Например, существуют задачи и алгоритмы на них, где в ходе перебора вершины постоянно «переобъединяются» в группы, а критерием для каждой группы является ее радиус. В этом случае радиус пересчитывается многократно, и скорость его поиска становится важным параметром. Как найти радиус быстрее?
Секрет в том, что для графов дорожных сетей все элементы просматривать не обязательно. На практике, достаточно просмотреть весьма малую часть всех строк.
Посмотрим, за счет чего это получается. Рассмотрим значения в одной строке матрицы МКР, другими словами, рассмотрим расстояния от одной вершины до всех остальных. Несложно доказать, что радиус графа не может быть больше чем максимальное значение в этой строке, и не может быть меньше чем минимальное значение в этой строке. Говоря математически, мы нашли верхнюю и нижнюю границу числа и если они совпадут – мы найдем число.
Допустим, мы нашли значения всего лишь в двух строках А и В. При этом, максимальное значение в строке А равно минимальному значению в строке В (эта величина будет стоять на пересечении столбца А и строки В). Несложно доказать, что А – центр графа, а найденное значение – его радиус. Задача решена.
Здорово, но такая ситуация на графах дорожных сетей маловероятна и решать задачу таким образом не получится. Поступим хитрее.
Возьмем пару строк В1 и В2. Из них сформируем вектор М таким образом: М(i)=max. Несложно доказать, что если для всех строк i значение min(M(i)) равно максимальному значению в столбце А, то, опять таки, А – центр, а найденное min(M(i)) – радиус.
Если пары строк окажется недостаточно, можно взять несколько строк, например три: B1, B2 и B3, тогда М(i)=max. Особенность графов дорожных сетей состоит в том, что много строк не понадобится (удастся уложиться в десяток). Это легко проверить, поэкспериментировав на существующих графах сетей, скачав их из интернета: ссылка .
В общем случае и с точки зрения математики это, конечно, не так. Вполне можно построить теоретический граф в котором придется использовать очень много строк В (почти все, кроме, А). Вот только невозможно построить реальную дорожную сеть такого вида - денег не хватит.
Осталась последняя задача. Как быстро найти эти удачные строки B1, B2 и т.д. Для графов реальных дорожных сетей это сделать очень просто и быстро. Это будут максимально удаленные друг от друга вершины, но не обязательно самые удаленные (говоря математически, находить диаметр графа нам не требуется). Берем любую вершину, находим для нее самую дальнюю, для новой опять самую дальнюю и так, пока пара вершин не окажется самой дальней друг для друга.
Мы получили пару вершин В1 и В2. Находим для пары вектор М, как описано выше. Строка, в которой мы нашли min(M(i)) - претендент на центр, обозначим его А. Если в столбце А значение min(M(i)) – максимальное, то уже найдены центр и радиус. Если же нет, значит максимальное значение в столбце А соответствует расстоянию до другой вершины (не B1 и не B2). Значит, мы получили новую вершину B3 в список на поиск вектора М. Как вариант, можно и для B3 поискать самую удаленную вершину и если она не В1 и не B2, добавить ее как В4. Таким образом, увеличиваем список вершин B, пока центр и радиус не будут найдены.
Более строго, с алгоритмом и нужными доказательствами этот алгоритм описан в , там же приведены результаты его использования на некоторых графах дорожных сетей США, а в ссылка и ссылка он описан менее академически, но более понятно.
Задача 2. Поиск матрицы кратчайших расстояний
Наиболее популярные алгоритмы поиска МКР (Флойда-Уоршелла, например) описаны . Все они универсальные, причем один из них – алгоритм Дейкстры с двоичной кучей – учитывает такое понятие как разреженный граф. Однако он тоже не использует особенности дорожных сетей.Мы будем их использовать и на совершенно другом алгоритме и на существующих графах получим ускорение в десятки раз по сравнению с алгоритмом Дейкстры. Заметим сразу, что особенность этого алгоритма в том, что ищет именно МКР, причем сразу всю и точно (т.е. не приближенно, не эвристически).
Рассмотрим основную идею алгоритма. Суть ее в том, чтобы удалять вершины графа без изменения кратчайших расстояний для оставшихся точек. Если мы будем так делать, запоминая к каким точкам и на каких расстояниях была присоединена удаленная вершина, то сможем удалить все точки, кроме одной, а потом собрать их обратно в граф, но с уже подсчитанными расстояниями.
Начнем с простого, с вершины со степенью 1. Ее можно удалить в любом случае. Через нее не проходит никаких кратчайших путей, кроме путей к самой вершине, причем идут они именно через ту вершину, к которой была присоединена удаляемая вершина.
Пусть А – вершина со степенью 2 и присоединена она в вершинам В1 и В2. Если маршрут В1-А-В2 длиннее или равен ребру В1-В2, через точку А не проходит никаких маршрутов, кроме маршрутов к самой точке А (все остальные проходят через В1-В2). Значит, точку А можно удалить. В ином случае, т.е. если В1-А-В2 короче В1-В2 или ребра В1-В2 вообще нет, вершину А можно удалить, установив вес ребра В1-В2 равным сумме весов: |В1-А|+|А-В2|. Маршрут от А до других точек проходит либо через В1, либо через В2, если будут известны расстояния для В1 и В2, расстояния от А так же легко вычислить.
По такому же принципу можно удалить вершину с любой степенью, заменяя, по мере необходимости, Вi-А-Вj на Bi-Bj. Правда, нужно понимать, что чем больше степень вершины, тем больше возможных ребер надо проверить. Для вершины степени n это число равно n(n-1)/2.
Теоретически, таким способом можно удалить все вершины в любом графе, однако, в общем случае, нас ждет неприятность, связанная с ростом числа ребер. При удалении вершины со степенью n, степень вершин, смежной с удаляемой, может: уменьшится на -1, не измениться, увеличится до n-2. Отсюда следует, что при удалении вершин со степенью 3 и выше, степень остальных вершин, в общем случае, растет, граф становится все менее разреженным и, в конце концов, удаление вершин превратится в довольно трудоемкую задачу. Алгоритм, в общем случае, является крайне трудоемким и практически бесполезным, но это именно в общем случае.
Графы дорожных сетей имеют уникальную особенность такого рода: многие вершины могут быть удалены не только без роста, но и с уменьшением степени смежных вершин. Причем, если некоторая вершина не может быть «успешно» удалена сейчас, она может быть «успешно» удалена позже, после удаления некоторых, смежных с ней вершин.
Соответственно, нам просто требуется на каждом шаге правильно выбирать вершины на удаление, начиная с тех, которые удаляются более «удачно».
Сам алгоритм более подробно можно посмотреть
Пусть - связный неориентированный граф. Так как любые две вершины графа и связаны, то существуют простые цепи с концами и . Таких цепей может быть несколько. Их длины являются неотрицательными целыми числами. Следовательно, между вершинами и должны существовать простые цепи наименьшей длины . Длина цепи наименьшей длины, связывающей вершины и , обозначается символом и называется расстоянием между вершинами и . По определению .
Нетрудно убедиться, что введенное таким образом понятие расстояния, удовлетворяет аксиомам метрики:
2. тогда и только тогда, когда ;
3. ![]() ;
;
4. справедливо неравенство треугольника:
Для фиксированной вершины графа расстояние до наиболее
удаленной от нее вершины: ![]() , называют
эксцентриситетом
(максимальным
удалением
)
вершины .
, называют
эксцентриситетом
(максимальным
удалением
)
вершины .
Диаметром графа называют число , равное расстоянию между наиболее удаленными друг от друга вершинами графа:
![]() .
.
Простая цепь, длина которой равна , называется диаметральной цепью . Очевидно, что диаметр графа равен наибольшему среди всех эксцентриситетов вершин графа. Вершина называется периферийной , если .
Минимальный из эксцентриситетов вершин связного графа называют его радиусом и обозначают :
Так как диаметр графа равен наибольшему из эксцентриситетов вершин, а радиус - наименьшему, то радиус графа не может быть больше его диаметра. Вершина называется центральной , если . Множество всех центральных вершин графа называют его центром . Центром графа может быть одна вершина или несколько вершин. Есть графы, центр которых совпадает с множеством всех его вершин. Например, центр простой цепи состоит из двух вершин при четном числе ее вершин и из одной - при нечетном, а у любого цикла все вершины являются центральными.
 Для иллюстрации обратимся к графу на рис.
4.29. Здесь
Для иллюстрации обратимся к графу на рис.
4.29. Здесь
Поэтому
Вершина 2 является центром графа, а все остальные его вершины - периферийные. Цепь 1, 2, 3 - одна из диаметральных цепей.
Для связного орграфа расстояние между вершинами и определяется как расстояние между вершинами и в неориентированном дубликате этого графа.
Задача нахождения центральных вершин графа постоянно встречается в практической деятельности. Пусть, например, вершины графа соответствуют небольшим поселкам, а его ребра - дорогам между ними. Требуется оптимально разместить по этим населенным пунктам, скажем, магазины. В подобных ситуациях критерий оптимальности обычно заключается в оптимизации «наихудшего» случая, то есть в минимизации расстояния от магазина до наиболее удаленного поселка. Такой подход к оптимизации предполагает размещение магазинов в поселках, которые представляют центральные вершины графа.
Обходы графов
Уже отмечалось, что начало теории графов связывают с задачей о кенигсбергских мостах. Эта знаменитая в свое время задача состоит в следующем. Семь мостов города Кенигсберга (ныне Калининграда) были расположены на реке Прегель так, как изображено на рис. 4.30. Задача состоит в том, чтобы, выйдя из дома, вернуться обратно, пройдя только один раз по каждому мосту.

Так как в задаче существенны только переходы через мосты, план города можно свести к изображению графа (точнее, мультиграфа), в котором ребра соответствуют мостам, а вершины - различным разделенным частям города, которые обозначены буквами (рис. 4.30, справа). Эйлер показал, что нельзя пройти по одному разу по всем кенигсбергским мостам и вернуться назад. В своей работе, опубликованной в 1736 году, он сформулировал и решил следующую общую проблему теории графов: при каких условиях связный граф содержит цикл, проходящий через каждое его ребро.
 Цикл в графе называется эйлеровым
,
если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл,
называется эйлеровым
графом. Такой граф можно нарисовать, не отрывая
карандаша от бумаги и не повторяя линий.
Цикл в графе называется эйлеровым
,
если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл,
называется эйлеровым
графом. Такой граф можно нарисовать, не отрывая
карандаша от бумаги и не повторяя линий.
Например, граф, изображенный на рис. 4.31, является эйлеровым, поскольку он содержит эйлеров цикл 1, 2, 3, 4, 5, 6, 4, 2, 6, 1. В этом графе есть и другие эйлеровы циклы. Ясно, что любые два таких цикла отличаются друг от друга только порядком обхода ребер.
Теорема 4.7. (Л. Эйлер, 1736 г.) Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
Цепь называется эйлеровой , если она содержит все ребра графа.
Теорема 4.8 (Л. Эйлер, 1736 г.) Мультиграф обладает эйлеровой цепью тогда и только тогда, когда он связен и число вершин нечетной степени равно 0 или 2.



Несмотря на «похожесть» в определениях для эйлеровых и гамильтоновых циклов, соответствующие теории, устанавливающие критерии существования и алгоритмы поиска таких циклов, имеют мало общего. Терема Эйлера (теорема 4.7) позволяет легко установить, является ли граф эйлеровым. Разработаны алгоритмы, позволяющие достаточно просто найти эйлеровы циклы эйлерова графа. Что касается гамильтоновых графов, то здесь положение дел существенно иное. Ответить на вопрос, является ли некий граф гамильтоновым, как правило, очень трудно. Общего критерия, подобного критерию Эйлера, здесь нет. Но, как оказалось, среди множества всех графов эйлеровых графов ничтожно мало, а вот гамильтоновых графов достаточно много.
Вычисление расстояний и определение маршрутов в графе являются одной из наиболее очевидных и практичных задач, которые возникают в теории графов. Введем некоторые необходимые определения.
Эксцентриситет вершины графа – расстояние до максимально удаленной от нее вершины. Для графа, для которого не определен вес его ребер, расстояние определяется в виде числа ребер.
Радиус графа – минимальный эксцентриситет вершин, а диаметр графа – максимальный эксцентриситет вершин.
Центр графа образуют вершины, у которых эксцентриситет равен радиусу. Центр графа может состоять из одной, нескольких или всех вершин графа.
Периферийные вершины имеют эксцентриситет, равный диаметру.
Простая цепь с длиной, равной диаметру графа, называется диаметральной .
Теорема 12.1. В связном графе диаметр не больше ранга его матрицы смежности.
Теорема 12.2. (Жордана) Каждое дерево имеет центр, состоящий из одной или двух смежных вершин.
Теорема 12.3. Если диаметр дерева четный, то дерево имеет единственный центр, и все диаметральные цепи проходят через него, если диаметр нечетный, то центров два и все диаметральные цепи содержат ребро, их соединяющее.
Очевидно практическое значение центра графа. Если, например, речь идет о графе дорог с вершинами-городами, то в математическом центре целесообразно размещать административный центр, складские помещения и т.п. Этот же подход можно применять и для взвешенного графа, где расстояния – это веса ребер. В качестве веса можно брать евклидовое расстояние, время или стоимость передвижения между пунктами.
Пример 12.5. Найти радиус, диаметр и центр графа, изображенного на рис. 12.1.
Решение. В данной задаче удобно использовать матрицу расстояний S . Элемент этой квадратной симметричной матрицы равен расстоянию между вершиной i и вершиной j . Для графа, показанного на рис. 12.1, матрица расстояний имеет следующий вид:
Вычислим эксцентриситет каждой вершины. Эту величину можно определить как максимальный элемент соответствующего столбца матрицы расстояний (или строки – поскольку матрица S симметрична). Получаем
Радиус графа r – минимальный эксцентриситет вершин. В данном случае r = 2. Такой эксцентриситет имеют вершины № 2, № 4 и № 5. Эти вершины образуют центр графа. Диаметр графа d – максимальный эксцентриситет вершин. В данном случае d = 3. Такой эксцентриситет имеют вершины № 1 и № 3, это периферия графа. В исследованном графе вершины оказались либо центральными, либо периферийными. В графах большего порядка существуют и другие вершины.
Эксцентриситеты вершин небольшого графа легко вычислять непосредственным подсчетом по рисунку. Однако не всегда граф задан своим рисунком. Кроме того, граф может иметь большой размер. Поэтому необходим другой способ решения предыдущей задачи. Известна следующая теорема.
Теорема 12.4. Пусть – матрица смежности графа G без петель и , где . Тогда равно числу маршрутов длины k от вершины к вершине .
Решение задач теории графов с помощью различных преобразований матрицы смежности называют алгебраическим методом .
Пример 12.6. Найти матрицу расстояний графа, изображенного на рис. 12.1, алгебраическим методом.
Решение. Матрица смежности данного графа равна:
Будем заполнять матрицу расстояний, рассматривая степени матрицы смежности. Единицы матрицы смежности показывают пары вершин, расстояние между которыми равно единице (т.е. они соединены одним ребром).
Диагональные элементы матрицы расстояний – нули. Умножаем матрицу смежности на себя:
Согласно теореме между вершинами 2 и 3, 1 и 4 и т.д. имеется некоторое число маршрутов длиной 2 (поскольку степень матрицы равна двум). Число маршрутов здесь не используется, важен сам факт наличия маршрута и его длина, на что и указывает ненулевой элемент степени матрицы, не совпадающий с элементом, отмеченным при вычислении маршрута меньшей длины. Проставляем 2 в незаполненные элементы матрицы расстояний и получаем следующее приближение:
Осталось неизвестным расстояние между вершинами 1 и 3. Будем умножать матрицу смежности саму на себя до тех пор, пока в матрице не появится ненулевой элемент . Тогда соответствующий элемент матрицы расстояний равен степени матрицы смежности: . На следующем шаге получаем
следовательно, , и окончательно
Полученная матрица совпадает с матрицей расстояний S (12.2), найденной непосредственными вычислениями по рисунку.